알아야 하는 이유
아날로그와 디지털은 우리 삶에서 땔레야 땔 수 없는, 아주 소중한 요소중 하나입니다.
이 둘이 있기에 수많은 전자기기가 탄생했고 우린 매일같이 그 전자기기들을 이용하고 있으니까요.
사실 사용하는 입장에서는 그 둘의 차이점을 알고 있지 않아도 상관없습니다.
하지만, 그것을 만들어야 하는 입장인 ― MAKER가 되기 위해 이 글을 보고 있는 ― 여러분들에겐 디지털과 아날로그는 꼭 알아야 할 개념입니다. (제 생각이긴 합니다)
전자제어 보드 중 비교적 난이도가 낮다고 알려진 아두이노(Arduino) 마저도 디지털과 아날로그에 대한 기본 지식이 깔려있지 않으면, 제대로 사용하지 못하기 때문이죠.
지금까지의 말로 인해서 벌써부터 어려울 것이라 생각할 수도 있지만, 그렇게 어렵지 않은 내용이니 편한 마음으로 읽다 보면 어느새 디지털/아날로그 박사가 되어있을 것입니다.
(보다가 이해가 안되는 것들이 있다면, 그건 쉬운걸 어렵게 설명하고 있는 제가 문제일 테니 댓글을 통해 질문 남겨주면 답변 남길게요)
시계로 보는 아날로그와 디지털
시계는 디지털 방식과 아날로그 방식 둘 다 존재하는 전자기기 중 가장 우리에게 익숙한 전자기기일 겁니다.
그래서 아날로그와 디지털을 설명하기에 아주 좋은 친구입니다.
저도 이 게시글에서 시계라는 좋은 친구를 통해 아날로그와 디지털을 설명하겠습니다.
아날로그시계와 연속성
아날로그는 간단하게 말하면 연속적입니다.
역시 이렇게 설명하면 어렵겠지요.
그럼 제 친구, 아날로그시계를 소개할 시간이겠네요.

이 친구는 아날로그 방식으로 시간을 알려줄 겁니다.
이제, 이 친구가 가리키고 있는 시간을 한 번 알아볼까요?
가장 두껍고 비교적 짧은 시침이 12와 1 사이를 가르키고 있으니 1시일 테고,
얇고 긴 분침이 2와 3 사이를 가리키고 있으니 10분에서 15분 사이일 것입니다.
그중에서도 3과 가장 가까우니, 1시 14분쯤 되어간다고 마무리 지어봅시다.
근데, 어딘가 찝찝하지 않나요?
분침이 3, 그러니까 15분에 가까워서 14분이라고 했는데, 그렇다고 정확히 14분이라고 단정 지을 수 있을까요?
혹은 어쩌면 14분과 15분 사이일 수도 있지 않을까요? 그러면 그 사이를 정확히 뭐로 부를 수 있을까요?
더 깊게 나아가 14분과 15분 사이에서도 14분에 완전 더 가깝다고 해봅시다. 그러면 14분 0초에서 10초 사이일 테죠.
그래도 의문은 풀리지 않습니다. 현미경까지 가져와본다면 그 답이 풀릴 수 있을까요?
답은 아닙니다. 계속해서 깊게 들어간다고 하더라도 우린 정확한 시간을 찾을 수 없을 겁니다.
(적분을 안다면, 위의 예시에 대한 이해가 빠를 겁니다 (아마,,))
이것이 바로 아날로그가 연속적이라는 것을 잘 설명해주는 사건입니다.
'연속적'이란 말은 "연달아 이어지는 것"을 뜻합니다.
우리가 위에서 시간을 구할 때 딱 맞아떨어지는 시간을 구할 수 없던 이유는 2와 3 사이에 연달아 이어지는 수많은 시간들, 또 그 시간들 사이에서도 연달아 이어지는 수많은 시간들이 존재했기 때문이었죠.
이것을 우리는 연속적이라고 합니다.
이제 아날로그가 연속적이라는 것에 대해 잘 이해가 되었나요?
지금 이해가 잘 안 되더라도 디지털을 알고 나면 그 차이가 명확해지면서 이해하는 데에 도움이 될 겁니다.
디지털시계와 불연속성
디지털은 불연속적입니다.
위에서 연속적이라는 것이 "연달아 이어지는 것"이라고 했으니, 불연속적이라는 것은 그렇지 않은 것이겠죠.
역시나 이번에도 이해를 돕기 위해 친구를 부르겠습니다.

이 친구는 디지털 방식으로 시간을 알려주는 디지털시계입니다.
이번에도 시간을 읽어볼까요?
...
네
15시 41분 00초네요.
의심의 여지가 없습니다.
정확하게 15시 41분 00초를 정확하게 가리키고 있습니다.
아날로그처럼 시간이 연달아 이어지기보다는 정확히 몇 시, 몇 분, 몇 초로 구분되어 떨어지는 것,
이것이 바로 디지털의 불연속성입니다.
그래프로 보는 디지털과 아날로그
이 부분은 특히 위의 내용보다 어려울 수 있습니다. 수학적인 지식이 조금 들어가거든요.
하지만 너무 걱정하지 마세요! 제가 핵심 내용은 '굵게' 처리해둘 테니 그 부분만 잘 이해해두시면 별 문제없을 거예요.
아날로그는 연속적이죠. 수가 연달아 이어집니다.
이에 반해 디지털은 불연속적입니다. 수가 구분되어 딱 끊어집니다.
시계에 벗어나서 좀 더 심화되어 알아가기 위해 그래프의 형태로 이를 표현해보겠습니다.
먼저, 1에서 3으로 다가가는 그래프를 좌표평면에 그려보려고 합니다. 각각의 방식으로요.
아래의 2 장의 사진이 바로 그 그래프입니다.

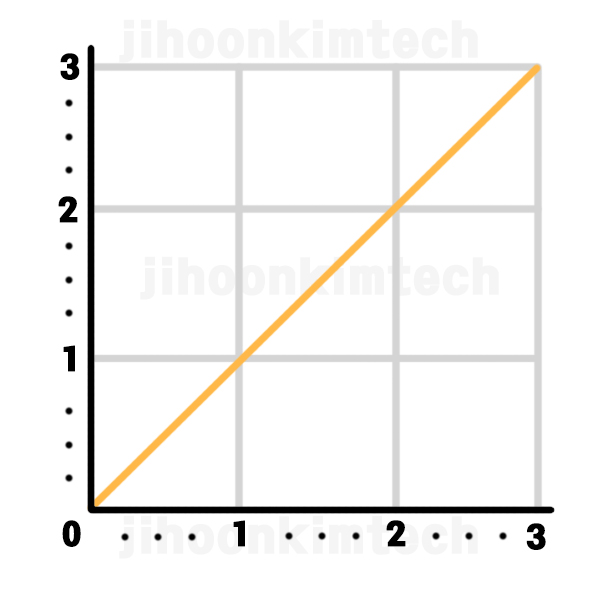
그래프를 보면 디지털은 계단식으로 끊겨 각져있고, 아날로그는 끊김 없이 부드럽게 대각을 그리며 이어집니다.
디지털은 불연속적입니다.
값이 정확하게 1, 2, 3으로 끊겨있고, 그렇기에 1, 2, 3을 제외한 나머지 좌표로는 이동할 수 없습니다.
그렇게 움직이려다 보니 그 사이를 가로지르지 못하고 계단을 그리며 3까지 나아갑니다.
이를 좌표로 표현하면 (0, 0)에서 출발해 (3, 3)까지 (0, 1), (1, 1), (1, 2), (2, 2) 이런 식으로 나아간다고 생각하면 됩니다.
반면 아날로그는 연속적이죠.
값이 1, 2, 3으로 끊기지 않고 그 사이에 연속되는 수들이 존재합니다.
이를테면 1과 2 사이에는 1.n부터 2.0이 있을 것이고, 또 그 사이에는 1.0n부터 2.00이 있겠죠. 물론 여기서 더 끝나지 않고 계속해서 수 사이에는 연속적으로 수가 존재할 테죠.

이 덕분에 각각의 수 사이에 무수히 연속되어 존재하는 또 다른 수들을 통해 부드럽게 나아갈 수 있는 것입니다.
이제 수학적(그렇게 수학적이진 않지만)으로도 연속적인 디지털과 불연속적인 아날로그를 정확히 알게 되었을 겁니다.
무엇이 다른가 하면..
전기적인 특성에서 디지털과 아날로그는 더 큰 차이를 보이지만, 이를 모두 이해하려면 높은 수준의 전공지식이 필요하기에 위에서 다룬 연속성과 불연속성에 따른 차이를 중점으로 다루겠습니다.
값의 표현
디지털은 딱 맞아떨어지는 값에 제한되는 것에 비해 아날로그는 수의 범위가 훨씬 넓습니다.
당연하게도 디지털이 표현하지 못하는 수를 아날로그는 거뜬히 표현할 수 있는 것이죠.
값의 정밀도
가령, 우리가 어떠한 물체의 길이를 재본다고 생각해봅시다.
디지털 방식으로 재면 값이 딱 떨어질 겁니다!
디지털 자의 성능이 소수점 두 자리 수면, 12.23 mm 이런 식으로 값이 나오겠죠?
그럼 아날로그 자를 사용해봅시다.
그럼 얼핏 봐서는 그 값이 어느 정도인지 감은 안 오겠지만, 당연하게도 아날로그는 연속적이므로 우리가 노력한 만큼 그 물체의 실제 사이즈에 최대한 근접하게 다가갈 수 있습니다.
실제 표현능력
위의 예시에서도 알 수 있듯이 우리가 '실제로 보기엔' 디지털이 더 잘 해석됩니다.
아날로그만큼 그 값을 세세히 표현하지는 못하지만, 적어도 어느 정도에 가까운지 명확하게 알려주기 때문이겠죠.
사실 아날로그 값이 가리키는 실제 값은 우리가 찾지 못할 겁니다.
우리가 계속해서 값을 찾아내더라도 그 사이에는 수많은 수가 연속적으로 존재할 테니까요.
시계의 예시만 하더라도 아날로그가 표현하고자 하는 값이 정확하게 얼마인지를 찾아가는 과정이 얼마나 피곤한 과정인지 알 수 있었습니다.
그래서 무엇을 써야 할까?
지금까지 우리는 아날로그와 디지털의 차이점을 분석하면서, 각각의 장단점을 알게 되었습니다.
디지털은 불연속적이기 때문에 각 값이 딱 끊겨 구분되고, 그로 인해 값이 표현할 수 있는 범위가 작습니다.
아날로그는 연속적이기 때문에 모든 수가 연속적으로 연달아 이어져 존재하고, 그로인해 값이 표현할 수 있는 범위가 매우 넓습니다.
이렇게만 보면 아날로그는 디지털보다 좋은 것으로 보일 수 있습니다.
하지만 우리가 실제 아날로그 값이 무엇을 가리키는지 살펴보는 과정에서 여러 고충을 겪으며, 우리의 눈으로 보았을 때는 비교적 덜 세밀하더라도 디지털 값이 더 명확할 수 있다는 것을 알게 되었죠.
그러면 우리는 뭘 사용해야 하는 것일까요?
그리고 디지털의 장점과 아날로그의 장점을 모두 섞은 완벽한 그 무언가는 없을까요?
답은 의외로 간단합니다.
디지털을 아날로그와 비슷하게 변환시키는 것입니다.
그것에 대해서는 다음 게시물에서 알아가도록 하겠습니다.